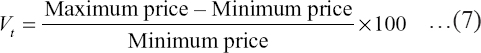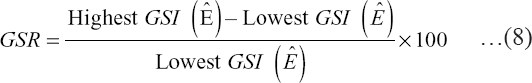| Experiment code | 19.9.3.51 |
|---|---|
| Experiment Title | Temporal Business Opportunities and Price Forecasting of Tomato, Onion and Potato (TOP) Vegetables for Major Markets of Gujarat Using Neural Network Model |
| Research Type | Departmental Research |
| Experiment Background | One of the most significant and well-known aspects of agriculture is seasonal variation. Seasonal variation is a cyclical pattern that repeats again every year (Sahu, 2018). Seasonal price variability, which is a significant issue for the agriculture industry, is the variation in price level over time (Barmon & Chaudhury, 2012). Production and availability are the two factors that affect an agricultural commodity's price (Camara, 2013). In general, the agriculture sector's income and price are unstable due to the nature and availability of agricultural commodities (Sahu, 2018). The majority of agricultural products, particularly fruits and vegetables, are highly perishable by nature and need to be marketed right once after being harvested. Timely marketing of such products is necessary to guarantee freshness and quality to consumers and to give growers a decent return on their investment (Kumar, Sharma, & Singh, 2005). Agricultural produce's price volatility is mostly brought on by its inelastic demand, significantly seasonal nature of production, and lengthy production cycles (Barmon & Chaudhury, 2012; Camara, 2013). Timmer (2011) also made the case that supply constraints, developing markets, rising demand, and untapped potential all have an impact on the price volatility of agricultural commodities. Farm price vary periodically and the price movement is similar from year to year (Rahn, 1968). The seasonal variation is the short time fluctuation occurring within a year in a time series data. Thus, the measurement of seasonal price variation is required to measure this fluctuation and determine the effect of season on price which in-turn help farmers for planning future production (Moniruzzaman, Islam, Sabur, Alam, & Alamgir, 2008). Agricultural prices generally follow a seasonal trend, with a seasonal low at harvest and an increase afterward. Due to fixed supply and demand depleting that supply, the price rises following harvest. Many scholars have noted the seasonality of price variation in vegetables. According to Noonari et al. (2015), the price of agricultural products, especially vegetables, was higher during the lean production season and lower during the post-harvest period. Similar to this, Mani et al. (2018) demonstrated the seasonality of tomato and ginger prices and came to the conclusion that prices peaked just before the following harvest and were lowest 1-2 months after harvest. For farmers, dealers, consumers, and the government, the high and unpredictable seasonal price unpredictability breeds uncertainty, raises risks, and influences unwise decisions (Barmon & Chaudhury, 2012). This price volatility could make small-scale farmers even more impoverished (FAO, 2011). But if farmers choose to sell their harvest at a higher price when the price rises, it can also boost their profit (Kilima, Mbiha, Erbaugh, & Larson, 2013). Price volatility is a significant contributor to profit that affects how people invest in commodities, how much money farms make, and how secure our food supply is. Farmers are negatively impacted by price fluctuations of a large size since they are unable to predict them. When a commodity's price is unusually high for a while, the area beneath it tends to grow as farmers are drawn to it in the hopes of earning a high income, which results in an oversupply and lowers the price (Nsumba, 2017). Commodity trade and price analysis both involve price forecasting. For the purpose of evaluating forecasting models, quantitative accuracy with minimal mistakes and turning point forecasting capacity are crucial. In the case of natural disasters like droughts, floods, and attacks by pests and diseases, the production and prices of agricultural commodities are frequently random and very unpredictable. Due to this, price modelling and forecasting are subject to a great deal of risk and uncertainty. Prices of agricultural products have a significant impact on consumers' ability to get food since they directly affect their real income, particularly for the poor who spend a major portion of their income on food. Policymakers require accurate estimates of predicted food costs in order to manage food security because food prices are a key factor in the fight against hunger. The government controlled food prices prior to the start of liberalisation and globalisation, making food price forecasting a poor value-added task. Currently, both domestic and international market pressures affect food prices. This causes a rise in price volatility and emphasises the need for accurate price forecasting methods. Farmers often depend on pricing estimates when making production and marketing choices that could have an impact on their finances months in the future. Due to several unique characteristics of the markets for agricultural products, agricultural price modelling differs from that of non-farm goods and services. Seasonal output, derived demand, and price-inelastic demand and supply functions are some of the distinguishing characteristics of agricultural products. The behaviour of agricultural product prices is significantly influenced by the biological nature of crop production. There are two fundamental methods for forecasting: structural models and time series models. The demand and supply schedules, as well as the equilibrium prices that follow from their crossing, are identified by the structural models by starting with the fundamental concepts of consumer and producer theory. The approaches used in structural modelling offer useful insights into the factors that affect how commodity prices change. In general, structural pricing forecasting requires significantly more computation and data than is often available in underdeveloped nations. As a result, when forecasting demands arise, researchers frequently turn to concise representations of price processes. Time series modelling is a key component of modern frugal price forecasting. For consistent and up-to-date price predictions, time series modelling requires less onerous data input. By using time series modelling, the same variable's prior observations are gathered and examined in order to create a model that describes the underlying relationship. Many resources have been used over the last few decades to create and enhance time series forecasting models. The Auto Regressive Integrated Moving Average (ARIMA) model is one of the most significant and popular time series models. The widely used Box-Jenkins approach and the statistical characteristics of the ARIMA model contribute to its popularity. Artificial neural network (ANN) modelling has gained a lot of interest recently as a substitute method for estimating and predicting in the fields of finance and economics (Zhang et al., 1998; Jha et al., 2009). A multivariate non-linear non-parametric self-adaptive statistical technique is known as an ANN. The fundamental benefits of neural networks are their adaptable functional structure and all-purpose functional approximator. A specific model form does not have to be specified for a given data set while using ANN. ANN has applications in a variety of disciplines, including biology, engineering, economics, etc. Kuan and White have examined the use of ANN in economics (1994). Hence, in order to assess the seasonality of price variation of Tomato, Onion and Potato (TOP) vegetables, to identify the temporary business opportunity in TOP vegetables, and to forecast Price of TOP vegetables for major markets of Gujarat, this study will carry out. The results of this study will assist policy makers in identifying seasonal changes in pricing and developing suitable policy responses, as well as farmers in understanding the seasonal pattern of major vegetables price and enabling them to implement appropriate production, storage, and sale strategies. |
| Experiment Group | Social Science |
| Unit Type | (01)RESEARCH UNIT |
| Unit | (41)AGRICULTURAL ECONOMICS (NAVSARI) |
| Department | (214)Economics |
| BudgetHead | (334/05018/00)334/12/REG/00698 |
| Objective |
|
| PI Name | (NAU-EMP-2019-000743)JAYDEEP VALLABHBHAI VARASANI |
| PI Email | jaydeepvarasani@nau.in |
| PI Mobile | 9512744888 |
| Year of Approval | 2023 |
| Commencement Year | 2023 |
| Completion Year | 2025 |
| Research Methodology |
Market: The market will be selected based on the largest amount of average yearly arrivals of the TOP vegetables in the market as well as the consistency with which the relevant time series data have been regularly available for a long time. Harvest and time frame: On the basis of area, production, and the significance of the vegetable crop for the area, the TOP vegetables crop is chosen for the study. The research will be carried by using data from wholesale price time series collected on a monthly basis between January, 2001 and October, 2024. Data: The Agricultural Produce Market Committee and AGMARKNET's secondary time series data on monthly TOP vegetables market prices will be used in the study.
Analytical Framework The following statistical tools will be used to assess the various objectives listed above. The seasonal character of price variations can be measured using a variety of techniques. The most popular technique for determining seasonal indexes is the ratio to moving average method (Meera & Sharma, 2016). The average seasonal price variation of commodities over a period of years, as indicated by a seasonal price index, can be used as a benchmark for comparison (Rahn, 1968). This approach reduces differences caused by causes other than seasonality by taking into account the effects of price inflation, cyclical production shifts, and technological advancement (Rahn, 1968; Flaskerud & Johnson, 2000). It aids in better purchasing, selling, and storage decisions and can be used to calculate agricultural storage profitability (Rahn, 1968; Jayaramu, 2015).
For the estimation of seasonal index, a 12-month moving average will be calculated as follows:
And the Centre Moving Average (CMA) was calculated as:
Seasonal index is the ratio of observed value of price (Yt) to centred moving average.
Where, E = Seasonal Factor or index Yt = Observed price in period t CMA = Centred Moving average. Seasonal Price Variation will be examined by calculating average seasonal index using monthly data where each month’s price/seasonal index (EA) will computed as the average of the same month’s seasonal index for all years included in the moving average time series. This will be calculated by arranging the seasonal indices month-wise for each year and calculating the average for each month. The indices are expressed as a percentage of the moving average price and adjusted to the base of 100 and is called Adjusted Seasonal Index or Grand Seasonal index (GSI). This will be calculated by multiplying each month’s average seasonal index by a correction factor as:
Where, The magnitude of price variability will be calculated as percentage of difference between highest and lowest de-seasonalized price in each year, as shown in following equation:
Where, Vt = magnitude of price variability in year t. The de-seasonalized price will be calculated by taking the ratio of actual price (Yt) to the average seasonal index (EA) for that month. The variability of price will be analyzed by calculating the average of price variability of each year.
Gross storage return (GSR) can be used to evaluate the feasibility of storage. Higher value of GSR indicates that the return to storage is higher in market and hence farmers can store commodity for future sale (Ngare, Simtowe, & Massingue, 2014). The GSR can be calculated by computing the percentage increase from seasonal low to seasonal high of Gross seasonal Index (Ngare et al. 2014; Mani et al. 2018). Mathematically, it can be computed as:
The higher percentage of GSR meant the return to storage for major vegetables will be higher in market and vice versa.
Model for a neural network by supplying the implicit functional representation of time, which allows a static neural network like the multilayer perceptron to be endowed with dynamic qualities, time series data can be described using ANN (Haykin, 1999). By incorporating either long-term or short-term memory, depending on the retention period, into the architecture of a static network, a neural network can be made dynamic. Time delay, which can be applied at the input layer of the neural network, is one straightforward method of incorporating short-term memory into the structure of a neural network. A Time-Delay Neural Network (TDNN) (Figure 1), used in the current study, is an illustration of such an architecture.
The number of layers and total number of nodes in each layer are both factors in the ANN construction for a specific time series prediction issue. As there is no theoretical foundation for calculating these characteristics, it is often discovered by experimentation. It has been demonstrated that neural networks with a single hidden layer are capable of approximating any non-linear function with the right amount of hidden layer nodes and training data. We employed a neural network with one hidden layer for this study. The number of input nodes that are lagged observations of the same variable is crucially important when performing time series analysis since it aids in modelling the autocorrelation structure of the data. The number of output nodes can be calculated quite easily. One output node has been employed in this study. Using an iterative process, multi-step forecasting is carried out using the Box-Jenkins ARIMA Time Series modelling approach. In order to forecast future value, this includes using the forecast value as an input. The model with fewer nodes in the hidden layer is always preferable because it performs better for out-of-sample forecasting and doesn't suffer from over-fitting. Equation (1) provides the general expression for the final output value yt+1 in a multi layer feed forward time delay neural network.
where, f and g denote the activation function at the hidden and output layers, respectively; p is the number of input nodes (tapped delay); q is the number of hidden nodes; βij is the weight attached to the connection between ith input node to the jth node of hidden layer; αj is the weight attached to the connection from the jth hidden node to the output node; and yt-i is the ith input (lag) of the model. Each node of the hidden layer receives the weighted sum of all the inputs, including a bias term for which the value of input variable will always be one. This weighted sum of input variables is then transformed by each hidden node using the activation function f which is usually a non-linear sigmoid function. In a similar manner, the output node also receives the weighted sum of the output of all the hidden nodes and produces an output by transforming the weighted sum using its activation function g. In the time series analysis, f is often chosen as the Logistic Sigmoid function and g, as an identity function. The logistic function is expressed as Equation (2):
For p tapped delay nodes, q hidden nodes, one output node and biases at both hidden and output layers, the total number of parameters (weights) in a three layer feed forward neural network is q(p + 2) + 1. For a univariate time series forecasting problem, the past observations of a given variable serve as input variables. The TDNN model attempts to map the following function:
where, yt+1 pertains to the observation at time t+1, p is the number of lagged observation, w is the vector of network weights, and εt+1 is the error-term at time t+1. Hence, TDNN acts like a non-linear autoregressive model.
The ARIMA Model
In an Auto-Regressive Integrated Moving Average (ARIMA) model, time series variable is assumed to be a linear function of the previous actual values and random shocks. In general, an ARIMA model is characterized by the notation ARIMA (p, d, q), where p, d and q denote orders of Auto-Regression (AR), Integration (differencing) and Moving Average (MA), respectively. ARIMA is a parsimonious approach which can represent both stationary and non-stationary processes. An ARMA (p, q) process is defined by Equation (4):
where, yt and εt are the actual value and random error at time period t, respectively, Φi (i=1, 2,……,p) and φi (j=1, 2,……,q) are the model parameters. The random errors, εt are assumed to be independently and identically distributed with a mean of zero and a constant variance of σ2.
The first step in the process of ARIMA modelling is to check for the stationarity of the series as the estimation procedure is available only for a stationary series. A series is regarded stationary if its statistical characteristics such as the mean and the autocorrelation structures are constant over time. The stochastic trend of the series is removed by differencing, while logarithmic transformation is employed to stabilize the variance. After appropriate transformation and differencing, multiple ARMA models are chosen on the basis of Auto-Correlation Function (ACF) and Partial Auto- Correlation Function (PACF) that closely fit the data. Then, the parameters of the tentative models are estimated through any non-linear optimization procedure such that the overall measure of errors is minimized or the likelihood function is maximized. Lastly, diagnostic checking for model adequacy is performed for all the estimated models through the plot of residual ACF and using Portmonteau test. The most suitable ARIMA model is selected using the smallest Akaike Information Criterion (AIC) or SchwarzBayesian Criterion (SBC) value and the lowest root mean square error (RMSE).
The Hybrid ARIMA - TDNN model
In this section, the time series decomposition is proposed in which ARIMA and TDNN models are combined in order to obtain a robust and efficient methodology for time series forecasting. Accordingly, we postulate that our time series data can be decomposed into a linear and a nonlinear component (Rojas et al., 2008), viz.
where, yt is the observed time series data, Lt is the linear auto-regressive component, and Nt is the non-linear component. In this approach, we apply an ARIMA model to the data series to fit the linear part and the residuals are modelled using neural network model only if there is an evidence of non-linearity for the series. Figure 2 shows a schematic diagram of this method. Let rt be the residual at time t of the linear component, then
where, L^ t is the estimate of the linear auto-regressive component. For non-linear components, we apply neural network model, i.e. where, p is the number of input delays and f is the nonlinear function. So the combined forecast is given by Equation (8):
where, εt is the error-term of the combined model at time t. Here, it is assumed that since ARIMA model cannot capture the nonlinear structure of the data, the residual of linear model will contain information about nonlinearity. Hence, the hybrid architecture is expected to exploit the feature and strength of both the models in order to improve the overall forecasting performance. The residuals which are obtained from fitted ARIMA model are utilized to test non linearity. The test statistic is given by Equation (9):
where, r(i) is the autocorrelation of the squared residuals, and h is the number of autocorrelations.
Forecast Evaluation Methods
The forecasting ability of different models will be assessed with respect to two common performance measures, viz. the root mean squared error (RMSE) and the mean absolute deviation (MAD). The RMSE measures the overall performance of a model and is given by Equation (10):
where, yt is the actual value for time t, y^ t is the predicted value for time t, and n is the number of predictions. The second criterion, the mean absolute deviation is a measure of average error for each point forecast and is given by Equation (11):
where the symbols have the same meaning as above. |
|
(NAU-EMP-2019-000743) JAYDEEP VALLABHBHAI VARASANI |
jaydeepvarasani@nau.in | 9512744888 | 11-10-2023 |
|
|
|
(NAU-EMP-1995-000728) JAYANTILAL JERAJBHAI MAKADIA |
jjmakadia@nau.in | 9825640825 | 11/10/2023 |
|
|
|
(NAU-EMP-2010-000269) NARENDRA SUMER SINGH |
ns_manohar@nau.in | 9427383049 | 11/10/2023 |
|
|
|
(NAU-EMP-2008-000398) ALPESHKUMAR KANTILAL LEUA |
alpeshleua@nau.in | 9725039457 | 11/10/2023 |
|
|
| Sr. No. | Operation Date | Nature of Data | Value of Data | Operation Status | |
|---|---|---|---|---|---|
| Sr. No. | Operation Date | Operation Status | |||
|---|---|---|---|---|---|
| Sr. No. | Operation Date | Operation Status | |||
|---|---|---|---|---|---|
| 1 | 22/01/2024 | In Progress | |||
| 2 | 28/01/2025 | In Progress | |||
| Sr. No. | Operation Date | Operation Status | |||
|---|---|---|---|---|---|
| 1 | 23/01/2024 | In Progress | |||
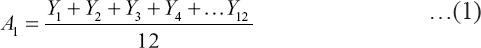
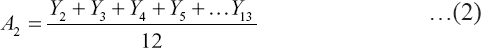
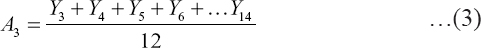


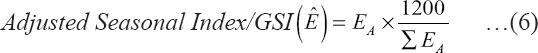
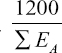 is the correction factor and, EA = Average Seasonal index for a month
is the correction factor and, EA = Average Seasonal index for a month